Topologie-Kriterium

[Frey und Field 1991] stellen einen relativ einfach in ein Programm einzubauenden Indikator für die Netzqualität vor, der als Winkelindikator interpretiert werden kann.

Definiert ist der Indikator für Dreiecke:

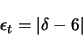$$\epsilon_t = \vert\delta - 6 \vert$$ (16)

Eine Anwendung auf Vierecknetze, Tetraeder und Hexaeder ist in der Literatur nicht vorgeschlagen, aber entsprechend der Tabelle 2.1 herleitbar.

Für Vierecke:

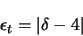$$\epsilon_t = \vert\delta - 4 \vert$$ (17)

Für Tetraeder:

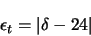$$\epsilon_t = \vert\delta - 24 \vert$$ (18)

Für Hexaeder:

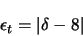$$\epsilon_t = \vert\delta - 8 \vert$$ (19)

Hierbei ist 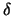$\delta$ die Anzahl der Elemente an einem Knoten. Ein optimales Netz, d.h. ein Dreiecknetz mit jeweils 6 Dreiecken pro Knoten oder ein Vierecknetz mit jeweils 4 Elementen je Knoten, hat 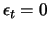$\epsilon_t = 0$. Die Qualität eines Netzes ist größer, je kleiner 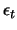$\epsilon_t$ ist.

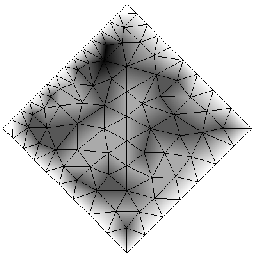
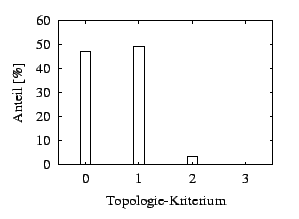
Abbildung 3.28: Topologie Kriterium a) Netz (grau $\hat{=}$ gute Qualität, schwarz $\hat{=}$ schlechte Qualität, weiß $\hat{=}$ Randknoten), b) Verteilung

a) b)
$\parbox{60mm}{\psfig{figure=kriterien/topo_k.ps,width=55mm}}$ $\parbox{70mm}{\psfig{figure=kriterien/topo_kriterium.eps,width=65mm}}$

Das Topologie-Kriterium ist ein Kriterium zum Auffinden von Knoten mit einer ungünstigen Anzahl von darauf referenzierenden Elementen. Diese Knoten sind irreguläre Punkte und lassen sich durch Topologieverbesserungen entsprechend Abschnitt 3.2.2 verbessern. Eine Verbesserung ist besonders bei Netzen aus Viereckelementen und Hexaederelementen sinnvoll, da dort jede Abweichung von der optimalen Anzahl sofort schlechtere Qualität nach den übrigen Kriterien darstellt. Irreguläre Punkte lassen sich in unstrukturierten Netzen nicht vermeiden. Zum einen sind sie zur Approximation der Geometrie notwendig, zum anderen ist eine lokale Verfeinerung nur durch irreguläre Punkte möglich. Anwendbar ist dieses Kriterium für alle Netze mit einer Elementart unter Berücksichtigung der Tabelle 2.1.