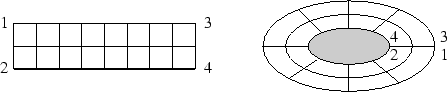 |
Die beiden dargestellten Algorithmen zur globalen Generierung von strukturierten Netzen können nur einfache Geometrien vernetzen. Zur Vernetzung komplizierterer Geometrien bietet die Multiblock-Methode die Möglichkeit, die Geometrie in einfachere, vernetzbare Teilgeometrien zu zerteilen, um diese dann hinterher mit einer der oben beschriebenen Vorgehensweisen zu vernetzen. Eine Anwendung des Verfahrens ist sowohl für zweidimensionale Dreieck- und Vierecknetze als auch für dreidimensionale Tetraeder- und Hexaedernetze möglich. Bei Dreieck- und Tetraedernetzen weisen die Elemente an den Teilungslinien bzw. -flächen eine schlechtere Qualität auf. Die betroffenen Knoten können unter Umständen sogar irregulär sein.
Die Geometrie wird in vernetzbare Teilgebiete aufgeteilt, die Blocks genannt werden. Diese Blocks werden nach dem Generieren der Teilnetze zum Multiblock zusammengefasst. Hierbei ist auf Kompatibilität an den Verbindungskanten der Teilnetze zu achten.
Eine Automatisierung des Aufteilungsprozesses ist nur teilweise möglich. Ein Ansatz hierfür ist die Mittelachsen- bzw. Mittelflächentechnik [Price u. a. 1995], [Price und Armstrong 1997] oder die Aufteilung unter Verwendung des eingeschlossenen Voronoi Graphen [Sheffer u. a. 1998]. In den meisten Fällen ist jedoch eine Steuerung der Aufteilung durch den Nutzer notwendig. Diese Notwendigkeit tritt besonders bei den Sonderfällen des Multiblock-Verfahrens, den O-, C- und H-Typ-Netzen, auf. Diese Typen von Netzen werden durch Zusammenlegen von jeweils zwei Knoten zu einem Netzknoten aus regelmäßigen Rechtecknetzen erzeugt. Verwendet werden diese Typen von Netzen um Löcher zu generieren, ohne Knoten zu erhalten, an denen die Anzahl der angrenzenden Elemente nicht der üblichen Anzahl entspricht. Die Buchstaben-Namen O für O-Typ, C für C-Typ und H für H-Typ entsprechen jeweils der Form der Netze.