Strukturierte Netze

Strukturierte Netze werden durch die folgende Definition beschrieben [Thompson u. a. 1999]:

Definition 1   Ein Elementnetz wird als strukturiert bezeichnet, wenn an allen inneren Knoten des Netzes regulär sind.

Ein regulärer Knoten wird wie folgt definiert [Thompson u. a. 1999]:

Definition 2   Ein Knoten wird als regulär bezeichnet, wenn die Anzahl der an ihn grenzenden Elemente die optimale Anzahl ist. Die optimale Anzahl von Elementen ergibt sich aus Tabelle 2.1.

Tabelle: Reguläre Punkte: Optimale Anzahl der an einen Knoten angrenzenden Elemente

Element-Typ	optimale Element-
	anzahl je Knoten
Dreieck	6
Viereck	4
Tetraeder	24
Hexaeder	8

Bei strukturierten Netzen ist, wie in Abbildung 2.1 a) dargestellt, die Anzahl der an einen Knoten angrenzenden Elemente für jeden inneren Knoten gleich und entsprechend der optimalen Anzahl.

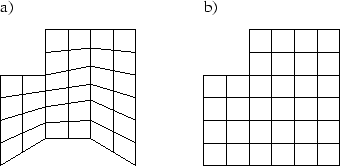
Strukturierte Netze können aus ein-, zwei- oder dreidimensionalen Elementen bestehen. Die Eckpunkte der Elemente liegen in einer strukturierten Ordnung vor. Eine Abbildung des Netzes auf ein Netz mit regelmäßigen Elementen ist möglich. Für ein Netz aus Viereckelementen ist die Abbildung auf ein Netz mit regelmäßigen Rechtecken in Abbildung 2.2 dargestellt.

Abbildung 2.2: a) Strukturiertes Netz, b) Abbildung des strukturierten Netzes