next up previous contents
Nächste Seite: Belastung auf Flächen Aufwärts: Belastungen Vorherige Seite: Belastungen   Inhalt

Belastung auf Linien

Für die Berechnung des Zuflusses aus einer Linie ist folgendes Integral zu lösen:


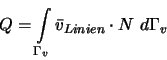
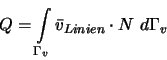
\begin{displaymath} Q = \int\limits_{\Gamma_v} \bar{v}_{Linien} \cdot N ~ d \Gamma_v \end{displaymath}

Hierbei sind als Formfunktionen $N$ die linearen Formfunktionen entsprechend Abbildung 5.13 einzusetzen. $\bar{v}$ ist der Volumenstrom senkrecht zum Rand und $\Gamma_v$ die Linie, längs der der Zufluss auftritt.

Abbildung 5.13: Lineare Formfunktion
\begin{figure} \centerline {\psfig{figure=formfunktionen/eindim.eps}} \end{figure}

Die Ersatzlasten in den Knoten, die aus Linienlasten entstehen, lassen sich durch das folgende Integral beschreiben:


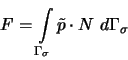
\begin{displaymath} F = \int\limits_{\Gamma_\sigma} \tilde{p} \cdot N ~ d \Gamma_\sigma \end{displaymath}

Hierbei sind $\tilde{p}$ die Linienlast und $\Gamma_\sigma$ die Linien, auf der die Last einwirkt. Zur Interpolation müssen hier die quadratischen Formfunktionen entsprechend Abbildung 5.14 verwendet werden.

Abbildung 5.14: Quadratische Formfunktion
\begin{figure} \centerline {\psfig{figure=formfunktionen/eindim2.eps}} \end{figure}