Parallele Netzgenerierung

Zur Parallelisierung der Netzgenerierung existiert ein Standardansatz, der unter anderem in [Rypl und Bittnar 1997], [Khan und Topping 1996] und [Wilson und Topping 1996] beschrieben wird. Dieser Ansatz ist für Dreieckelemente, Viereckelemente und Tetraederelemente anwendbar. Netzgeneratoren für Hexaederelemente lassen sich mit dem beschriebenen Ansatz nicht parallelisieren, da Knoten und Kanten auf den Teilgebietsgrenzen vorgegeben werden müssen und zur Zeit noch kein Algorithmus vorliegt, der diese Eigenschaft erfüllt. Zur Generierung der Netze sind die folgenden Schritte notwendig:

Schritt 1:

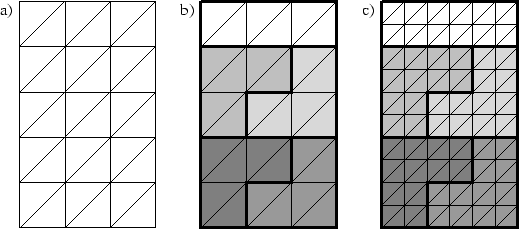
Ein grobes Hintergrundnetz wird unter Zuhilfenahme des gewählten Algorithmus erzeugt. Dieses Hintergrundnetz muss alle geometrischen Bedingungen, die das endgültige Netz berücksichtigen soll, erfüllen. Des weiteren sollten alle Elemente des temporär vorliegenden Netzes eine ähnliche Größe aufweisen. Ein Beispiel für ein Ausgangsnetz ist in Abbildung 2.20 a) dargestellt.

Schritt 2:

Das Ausgangsnetz wird im nächsten Schritt in $n$ Teilgebiete zerteilt. Hierfür werden Algorithmen, wie in Abschnitt 2.3 beschriebenen, verwendet. $n$ ist hierbei Anzahl der zur Verfügung stehenden Prozessoren. (siehe Abbildung 2.20 b))

Schritt 3:

Die Teilnetze werden parallel auf den Prozessoren verfeinert. Hierbei ist an den Koppelkanten die Kompatibilität der Teilnetze zu berücksichtigen, die eine gewisse Kommunikation zwischen den Prozessoren erfordert oder durch Vorgabe der Knoten auf den Gebietsgrenzen realisiert werden kann. Eine Glättung innerhalb der Teilgebiete ist notwendig. (siehe Abbildung 2.20 c))

Abbildung 2.20: Parallele Netzgenerierung: a) grobes Netz, b) Partitioniertes Netz, c) feines Finite-Elemente-Netz

Eine alternative Methode zur parallelen Generierung von Elementnetzen stellt [Mitchell und Vavasis 1997] für den n-dimensionalen Fall dar, die [Meißner u. a. 1996] für zweidimensionale Netze beschreiben. Hierbei wird die Originalgeometrie rekursiv in mehrere Teile geteilt und eine Randdiskretisierung für jedes Teilgebiet vorgegeben. Eine parallele Vernetzung der Teilgebiete ist anschließend ohne Kommunikation möglich, wodurch eine sehr gute Effizienz der parallelen Netzgenerierung erreicht wird.