


Nächste Seite: Divide-and-Conquer-Algorithmus:
Aufwärts: Statische Algorithmen
Vorherige Seite: Statische Algorithmen
Inhalt
Recursive-Split-Algorithmus:
Dieser Algorithmus wurde zuerst von [Lewis und Robinson 1978] beschrieben und besteht aus folgenden Schritten:
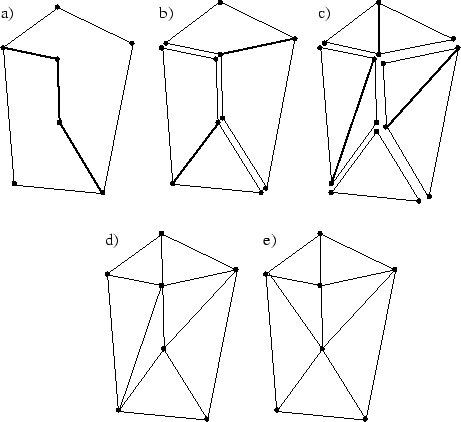
Abbildung 3.5:
Recursive-Split-Algorithmus
 |
- Schritt 1:
- Der umschließende Polygonzug wird gesucht.
- Schritt 2:
- Rekursiv wird die Geometrie in jeweils zwei Teilgeometrien zerlegt, die möglichst kreisförmig sind (Abbildung 3.5a)-d)). Abgebrochen wird die Rekursion, wenn alle Teilgeometrien nur noch aus drei Punkten bestehen.
- Schritt 3:
- Über alle Kanten wird traversiert. Die beiden durch diese Kante benachbarten Dreiecke werden zu einem gedachten Viereck zusammengefasst. Entlang der kürzeren Kante wird das Viereck dann in zwei Dreiecke zerteilt. Dieser Schritt wird solange wiederholt, bis keine Änderungen mehr auftreten (Abbildung 3.5e)).
Für diesen Algorithmus sind die Laufzeitangaben in der Literatur verschieden. Während [Lewis und Robinson 1978] von einem Laufzeitverhalten von
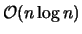 schreiben, nehmen [Lee und Schachter 1980] ein Laufzeitverhalten von
schreiben, nehmen [Lee und Schachter 1980] ein Laufzeitverhalten von 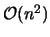 an. Beide Angaben sind nicht beweisbar. Die Bisektion zeigt eine direkte Parallelisierbarkeit des Algorithmus auf.
an. Beide Angaben sind nicht beweisbar. Die Bisektion zeigt eine direkte Parallelisierbarkeit des Algorithmus auf.

![]() schreiben, nehmen [Lee und Schachter 1980] ein Laufzeitverhalten von
schreiben, nehmen [Lee und Schachter 1980] ein Laufzeitverhalten von ![]() an. Beide Angaben sind nicht beweisbar. Die Bisektion zeigt eine direkte Parallelisierbarkeit des Algorithmus auf.
an. Beide Angaben sind nicht beweisbar. Die Bisektion zeigt eine direkte Parallelisierbarkeit des Algorithmus auf.