


Nächste Seite: Watson's Algorithmus:
Aufwärts: Dynamische Algorithmen
Vorherige Seite: Dynamische Algorithmen
Inhalt
Incremental-Algorithmus:
Dieser Algorithmus wurde unter anderem von [Lee und Schachter 1980] vorgestellt.
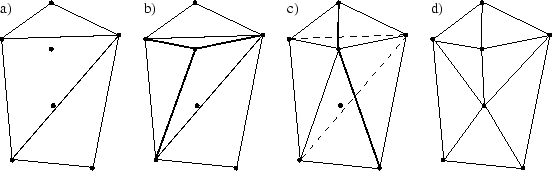
Abbildung 3.9:
Incremental-Algorithmus
 |
- Schritt 1:
- Es muss eine grobe initiale Triangulierung erzeugt werden. Dies kann z.B. durch die Triangulierung des umschließenden Polygonzugs geschehen (Abbildung 3.9 a)).
- Schritt 2:
- Ein Punkt wird eingefügt, indem das Dreieck, in dem der Punkt liegt, durch drei neue Dreiecke, bestehend aus dem einzubindenden Punkt und den alten Punkten des Dreiecks, ersetzt wird (Abbildung 3.9 b)).
- Schritt 3:
- Alle Vierecke, die sich aus Dreiecken, die Kanten des alten aufgelösten Dreiecks besitzen, bilden lassen, müssen überprüft und möglicherweise muss die diagonale Kante getauscht werden (Abbildung 3.9 c)).
Für diesen Algorithmus sind die Angaben über das Laufzeitverhalten in der Literatur unterschiedlich. Während die meisten Angaben hierfür 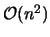 lauten, ist in [Heller 1990] ein Laufzeitverhalten von
lauten, ist in [Heller 1990] ein Laufzeitverhalten von
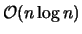 angegeben.
angegeben.

![]() lauten, ist in [Heller 1990] ein Laufzeitverhalten von
lauten, ist in [Heller 1990] ein Laufzeitverhalten von
![]() angegeben.
angegeben.