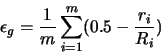 |
(26) |
[Shimada u. a. 1997] schlagen zum Bewerten von Netzen ein Geometrie-Kriterium vor. Dieses ist definiert durch:
Das Geometrie-Kriterium teilt den Innenkreisradius durch den Umkreisradius. Die Erweiterung des Kriteriums ist problemlos für Tetraeder möglich. Hierbei müssen die Radien der Kreise nur durch die Radien der Kugeln ersetzt werden.
|
Dieses Verhältnis des Innenkreises zum Umkreis ist für gleichseitige Dreiecke ![]() und für stumpfwinklige Dreiecke strebt es gegen
und für stumpfwinklige Dreiecke strebt es gegen ![]() . Je kleiner der Indikator
. Je kleiner der Indikator ![]() ist, desto regulärer ist das jeweilige Element. Als obere Grenze kann der Indikator den Wert 1 annehmen. Dreiecke mit einem spitzen Innenwinkel werden schlecht erkannt.
ist, desto regulärer ist das jeweilige Element. Als obere Grenze kann der Indikator den Wert 1 annehmen. Dreiecke mit einem spitzen Innenwinkel werden schlecht erkannt.
Die Verteilung der Qualität der Elemente ist entsprechend Abbildung 3.33 b) meist quadratisch bis logarithmisch, wodurch auch relativ schlechte Elemente kaum aufgespürt werden können. Der Wertebereich ist normiert. Eine Anwendung des Indikators ist nur für Dreiecke und Tetraeder möglich.