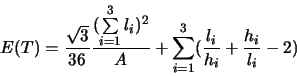Gemischter Indikator

Ein gemischter Indikator wird von [Schöberl 1997] vorgestellt. Dieser Indikator kann zum einen ungünstige Elemente aufspüren, aber auch die Qualität eines gesamten Netzwerkes beurteilen. Die Qualität eines Dreiecks wird mit:

$$E(T) = \frac{\sqrt{3}}{36} \frac{( \sum\limits_{i=1}^3 l_i )^2}{ A} + \sum\limits_{i=1}^3(\frac{l_i}{h_i}+\frac{h_i}{l_i}-2)$$ (27)

und die Qualität eines Tetraeder mit:

$$E(T) = \frac{1}{6^4\sqrt{2}} \frac{( \sum\limits_{i=1}^3 l_... ...}{ V} + \sum\limits_{i=1}^3(\frac{l_i}{h_i}+\frac{h_i}{l_i}-2)$$ (28)

berechnet. Hierbei sind $l_i$ die Kantenlängen und $h_i$ die zugehörigen Höhen, A die Dreieckfläche und V das Volumen. Der Optimalwert von $E(T)$ ist 1, ungünstige Triangulierungen bzw. Elemente haben größere Werte. Eine obere Schranke kann nicht angegeben werden.

Abbildung 3.34: Gemischter Indikator a) Netz (weiß $\hat{=}$ gute Qualität, schwarz $\hat{=}$ schlechte Qualität), b) Verteilung

a) b)
$\parbox{60mm}{\psfig{figure=kriterien/gemischt_k.ps,width=55mm}}$ $\parbox{70mm}{\psfig{figure=kriterien/gemischt_kriterium.eps,width=65mm}}$

Der in Gleichung 3.14 dargestellte Indikator besteht aus zwei Teilen. Der erste Teil 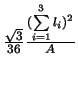$\frac{\sqrt{3}}{36} \frac{( \sum\limits_{i=1}^3 l_i )^2}{ A}$ sucht nach stumpfwinkligen Elementen, der zweite Teil 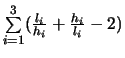$\sum\limits_{i=1}^3(\frac{l_i}{h_i}+\frac{h_i}{l_i}-2)$ nach Elementen mit kleinem Innenwinkel.

Die Verteilung der Qualität der Elemente ist entsprechend Abbildung 3.34 b) meist linear bis quadratisch. Eine Normierung des Wertebereichs ist nicht vorhanden, wodurch das Aufspüren relativ schlechter Elemente erschwert wird. Das gleichzeitige Bewerten nach zwei Kriterien hat Vor- und Nachteile. Eine Optimierung nach mehreren Kriterien ist allgemein immer sinnvoll. Durch die Mischung ist nicht festzustellen welches Teilkriterium verletzt wird. Eine Teilung des Kriteriums in zwei Teilkriterien, für die jeweils die Qualität bestimmt wird, erscheint sinnvoll. Eine Anwendung des Indikators ist nur für Dreiecke und Tetraeder möglich.