 |
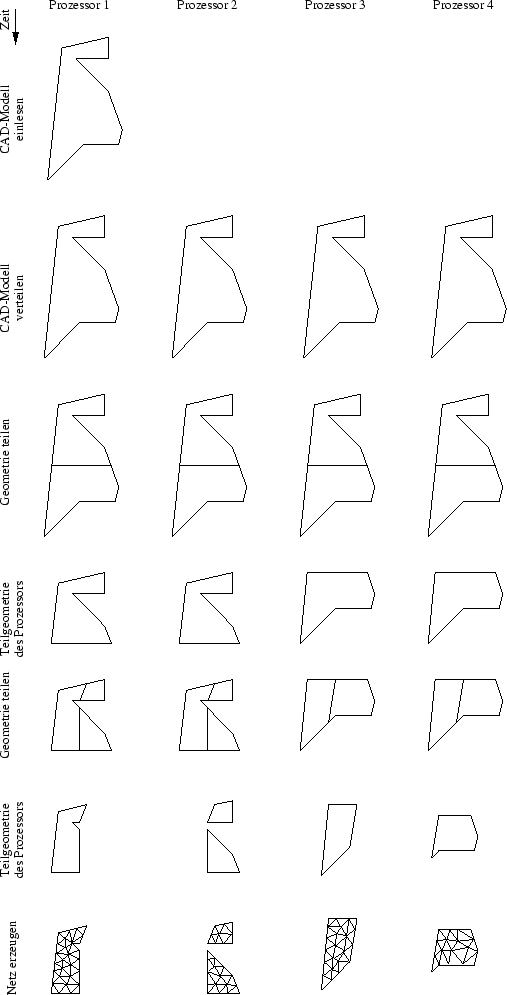
Der parallele Ablauf der Netzgenerierung ist schematisch in Abbildung 6.12 für die Vernetzung mit vier Prozessoren abgebildet. Zu Beginn liest ein Prozessor das CAD-Modell ein. Anschließend werden die Daten durch eine Kommunikation den anderen Prozessoren zur Verfügung gestellt. Jeder Prozessor diskretisiert als nächstes den Gebietsrand sowie Linien und Löcher entsprechend der Verteilungsfunktion der Netzdichte. Parallel wird anschließend eine Teilungslinie unter Verwendung der Schwerachsenmethode ermittelt. Die Geometrie wird geteilt, wobei der nicht benötigte Teil der Geometrie gelöscht und die Teilungslinie als Kante in die Geometrie eingebaut werden. Die Diskretisierung der Teilungslinie ist anschließend erforderlich. Rekursiv wird das Teilen der Geometrie und das Diskretisieren der Teilungslinie solange wiederholt, bis jeder Prozessor nur noch die Teilgeometrie hat, die er vernetzen muss. Anschließend wird das Netz parallel generiert.
Das Zustandsdiagramm in Abbildung 6.13 stellt die einzelnen Schritte der parallelen Netzgenerierung auf einem Prozessor genauer dar. Zuerst wird die Grundgeometrie aufgebaut. Wie schon beschrieben, ist es notwendig, eine Diskretisierung auf allen Kanten der Geometrie vorzunehmen, um die Kommunikation zwischen den Prozessoren zu vermeiden. Dies geschieht, indem auf allen Kanten Knoten im Abstand entsprechend der Wichtungsfunktion eingefügt werden. Als nächstes wird ein grobes Dreiecknetz erzeugt, bei dem sich die Eckpunkte der Dreiecke in den Eckpunkten der Geometrie befinden. Unter Verwendung dieses groben Netzes können die Flächenintegrale für den Schwerpunkt und die Trägheitsmomente berechnet werden.
In den nächsten Schritten wird zuerst der Ursprung der Geometrie in den Schwerpunkt verschoben. Unter Verwendung der Hauptachsen wird die Schnittlinie ermittelt und die Geometrie daran geteilt. Anschließend ist entlang des Schnittes eine Diskretisierung der Kanten notwendig. Falls eine weitere rekursive Teilung notwendig ist, d.h. wenn die Rekursionsanzahl kleiner ist als die Dimension des zur Verfügung stehenden Hypercubes des Parallelrechners, folgt eine erneute Vernetzung mit Dreiecken, um die Flächenintegrale für die aktuelle Geometrie zu berechnen. Ist eine weitere Teilung nicht notwendig, wird direkt ein Dreiecknetz erzeugt.
Für Viereckelemente und Hexaederelemente ist als nächstes eine Umwandlung des Dreiecknetzes in ein Vierecknetz notwendig. Dies wird auf die in Abschnitt 3.1.4 beschriebene Art durchgeführt. Eine Glättung und Verbesserung des Netzes nach Abschnitt 3.2 unter Berücksichtigung der Qualitätskriterien ist anschließend notwendig.
Als nächstes werden für Prismaelemente und Hexaederelemente die Knoten in der Tiefe unter Berücksichtigung aller geometrischen Bedingungen erzeugt. Unter Verwendung der neu entstandenen Knoten werden aus den ebenen Elementen dreidimensionale Elemente erzeugt.
Anschließend ist der Einbau einer lokalen Verfeinerung nach Abschnitt 3.3 möglich, bevor die Randbedingungen für die Finite-Elemente-Berechnung den Netzknoten zugewiesen werden. Als Abschluss der Netzgenerierung wird das Netz entweder in eine Datei geschrieben oder die Daten werden direkt einem anderen Programm zur Verfügung gestellt.