Geometrisch sortierte Datenstrukturen

Zur Verwaltung der Finiten-Elemente und deren Knoten gibt es verschiedene Herangehensweisen. In vielen älteren Finite-Elemente-Programmen werden hierfür meistens Felder, in neueren Programmen oft auch Listen verwendet. Für Finite-Elemente-Programme ist dies auch in der Regel ausreichend, da ein geometrisches Suchen nach Elementen oder Knoten nicht notwendig ist. Für Netzgenerierungsprogramme sind Felder und Listen allerdings unzureichend, da hier häufig geometrisch nach Knoten oder Elementen, wie z.B. bei der Einarbeitung von Randbedingungen, gesucht werden muss.

Abbildung 6.6: Quadtree-Struktur

Geometrisch sortierte Datenstrukturen sind im eindimensionalen Fall Binärbäume, im zweidimensionalen Fall Quadtree-Strukturen und im dreidimensionalen Fall Octree-Strukturen. Am Beispiel der Quadtree-Struktur wird nun die Funktionsweise dieser geometrisch sortierten Datenstrukturen demonstriert. Binärbäume und Octree-Strukturen funktionieren ihrer Dimensionalität entsprechend.

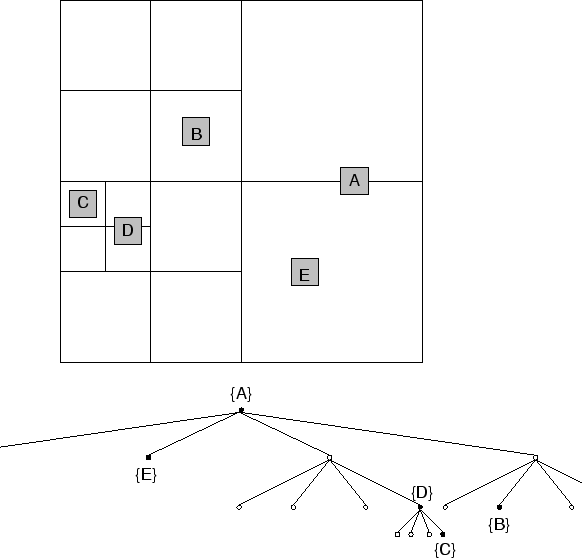
In Abbildung 6.6 sind einzelne Finite-Elemente eines Netzes und der zugehörige Quadtree dargestellt. Für das Gebiet, in dem sich die Elemente befinden, wird ein umschließendes Rechteck mit achsenparallelen Kanten gesucht. Dieses Rechteck wird rekursiv in jeweils vier gleich große Rechtecke geteilt, solange Elemente in eins der jeweiligen Teilrechtecke passen. Jedes Viereck besitzt eine Liste mit Elementen sowie vier Zeiger auf Vierecke, die Teile dieses Vierecks sind. Elemente, die nicht vollständig in eines der unteren Vierecke passen, werden in der Liste abgelegt, die anderen den jeweiligen Vierecken zugeordnet und dort rekursiv weiter sortiert. So ist in Abbildung 6.6 das Elemente A nur der obersten Ebene zuzuordnen, während das Element C in der 3. Unterebene einzusortieren ist. Beim geometrischen Suchen in einem Quadtree ist jeweils nur ein Ast der Baumstruktur abzusuchen, weshalb sich gerade bei großen Datenmengen enorme Zeitvorteile ergeben.

Abbildung 6.7: Netze zum Vergleichen der Zugriffszeiten

$\parbox{4cm}{a)}$ $\parbox{5cm}{b)}$ $\parbox{5cm}{ c)}$$\parbox{4cm}{\psfig{figure=quad/z60_2_netz.eps,width=40mm}}$ $\parbox{5cm}{\psfig{figure=quad/z61_netz.ps,width=50mm}}$ $\parbox{5cm}{\psfig{figure=quad/z62_netz.ps,width=50mm}}$

Die Anwendbarkeit der geometrisch sortierten Datenstrukturen wurde an verschiedenen Beispielen untersucht. Am Beispiel eines Quadrates mit $24\times 24$ Elementen (Abbildung 6.7 a)), eines Quaders mit $24 \times 24 \times 33$ Elementen (Abbildung 6.7 b)), eines Quaders mit $24 \times 24 \times 10$ Elementen (Abbildung 6.7 c)) und des Baugrundmodells des TREPTOWERS in Berlin aus Abschnitt 7.2 mit 49442 Elementen soll die Anwendbarkeit gezeigt werden.

Als Abbruchkriterium beim Aufbauen der Quadtree-Struktur für Finite-Elemente ist festgelegt, dass sie komplett innerhalb des Vierecks liegen müssen, um hinterher auch wieder gefunden werden zu können. Knoten können in beliebig kleine Gebiete einsortiert werden um wieder gefunden zu werden. Als Abbruchkriterium ist hier daher festgelegt, dass nicht mehr als 10 Knoten in einem Viereck vorhanden sein dürfen.

Abbildung 6.8: Zeiten zum Suchen in der Datenstruktur für ein Quadrat mit $24\times 24$ Elementen

$\parbox{6cm}{\psfig{figure=quad/z60a.eps}}$$\parbox{6cm}{ \begin{tabular}{r\vert\vert l\vert l} Datenstruktur &... ....037173 & 0.022337 \\ Quadtree & 0.000612974 & 0.00041604 \\ \end{tabular}}$

Das zeitliche Verhalten für das Suchen nach einem Viereckelement für das 1. Beispiel ist in Abbildung 6.8 dargestellt. Gesucht wurde jeweils 100 mal nach einem Knoten bzw. nach einem Element. Der Vorteil der Quadtree-Struktur ist deutlich zu erkennen. Die Suchzeiten für Elemente im Quadtree betragen nur $\frac{1}{60}$ der Suchzeit der Elemente in der Liste. Für Knoten ergibt sich das Verhältnis $\frac{1}{53}$.

Abbildung 6.9: Zeiten zum Suchen in der Datenstruktur für einen Quader mit $24 \times 24 \times 33$ Elementen

$\parbox{6cm}{\psfig{figure=quad/z61a.eps}}$$\parbox{6cm}{ \begin{tabular}{r\vert\vert l\vert l} Datenstruktur &... ... & 0.014055 & 0.00165892\\ Octree & 0.017451 & 0.000589013\\ \end{tabular}}$

Abbildung 6.10: Zeiten zum Suchen in der Datenstruktur für einen Quader mit $24 \times 24 \times 10$ Elementen

$\parbox{6cm}{\psfig{figure=quad/z62a.eps}}$$\parbox{6cm}{ \begin{tabular}{r\vert\vert l\vert l} Datenstruktur &... ...0.00389004 & 0.000772953\\ Octree & 0.018182 & 0.000566959\\ \end{tabular}}$

In Abbildung 6.9 sind die Zeiten für 100 mal Suchen in Listen-, Quadtree- und Octree-Struktur für das 2. Beispiel dargestellt. Die Suche nach einem Element ist mit der Quadtree-Struktur am schnellsten, gefolgt von der Octree-Struktur. Die Verhältnisse zur Suchzeit in der Liste sind $\frac{1}{191}$ bzw. $\frac{1}{154}$. Für die Knoten ist die schnellste Suche in der Octree-Struktur möglich. Die Verhältnisse zur Liste sind hier: $\frac{1}{778}$ und $\frac{1}{2232}$.

Finite-Elemente-Modelle von Baugrundstrukturen haben in der Regel eine geringe Tiefe im Vergleich zu den restlichen Ausdehnungen des Modells. Dies wird mit dem Beispiel 3 nachgebildet. Das Verhältnis der Zugriffszeiten (Abbildung 6.10) für die Suche nach Elementen ist für den Quadtree $\frac{1}{204}$ und für den Octree $\frac{1}{43}$ im Vergleich zu den Zeiten in der Liste. Für die Suche nach Knoten sind die Verhältnisse $\frac{1}{532}$ und $\frac{1}{726}$. Hierbei sieht man deutlich, dass die Suche im Octree trotz seines dreidimensionalen Zugriffs nicht schneller ist als das Suchen im Quadtree.

Abbildung 6.11: Zeiten zum Suchen in der Datenstruktur für ein Baugrundmodell mit 49442 Elementen

$\parbox{6cm}{\psfig{figure=quad/s5a.eps}}$$\parbox{6cm}{ \small \begin{tabular}{r\vert\vert l\vert l\vert\vert ... ...48 & 9 & 0.00093 & 10 \\ Octree & 0.379 & 7 & 0.00057 & 8 \\ \end{tabular}}$

Das Beispiel Treptower zeigt ähnliche Verhältnisse für die Zugriffszeiten (Abbildung 6.11). Die Zeit zum Suchen nach einem Knoten im Quadtree beträgt $\frac{1}{28}$ der Zeit für die Liste, die Zeit für den Octree ist $\frac{1}{19}$. Die Suche nach einem Knoten ist auch für dieses Beispiel deutlich schneller mit dem Octree. Hierbei ist das Verhältnis zur Zeit der Liste $\frac{1}{7937}$. Das Verhältnis Suchzeit im Quadtree zur Suchzeit in der Liste ist $\frac{1}{4949}$.

Ein Zeitvorteil der Octree-Struktur gegenüber der Quadtree-Struktur kann nur für Knoten, aber nicht für Elemente gezeigt werden. Erklären lässt sich dies durch die Abmaße der Geometrie der Beispiele. Bei würfelförmigen Geometrien und würfelförmigen Elementen, wie in Beispiel 2, stellt der Octree eine Alternative zur Liste für die Suche nach Elementen dar. Sind die Abmessungen der Geometrie nicht würfelförmig, sondern ist eine Kante des umschließenden Quaders groß oder klein gegenüber den anderen Kanten, haben die Teilquader ebenfalls unausgewogene Seitenverhältnisse. Die Octree-Struktur kann dann nur mit einer sehr geringen Anzahl von Ebenen erzeugt werden, da die Elemente in einer Richtung schon nach wenigen Rekursionen nicht mehr in die Teilquader passen. Der gleiche Effekt ist bei Elementen zu finden, die in einer Richtung lang oder kurz gegenüber den anderen Richtungen sind. Die Elemente lassen sich schlecht in untere Ebenen eine Octrees einordnen, da sie in einer Koordinatenrichtung in der Regel nicht in einen Teilquader passen. In Abbildung 6.11 sind die Anzahlen der Ebenen für die Quadtree-Struktur und die der Octree-Struktur für das Beispiel TREPTOWERS dargestellt. Die Quadtree-Struktur hat zwei Ebenen mehr, wodurch die Anzahl der Elemente, die in der untersten Ebene überprüft werden müssen, sich auf etwa $\frac{1}{16}$ der Anzahl der Elemente, die sich in der Octree-Struktur befinden, reduziert. Bei Finite-Elemente-Modellen aus dem Bereich der Geotechnik, die mit einer Projektionstechnik erstellt wurden, ist die Tiefe der Modelle meist klein gegenüber den übrigen Ausmaßen. Oft haben die Elemente auch eine säulenartige Form. Hierbei hat sich der Quadtree gegenüber dem Octree als deutlich bessere Datenstruktur zur Verwaltung der Elemente erwiesen.