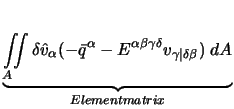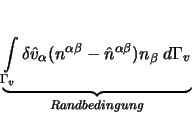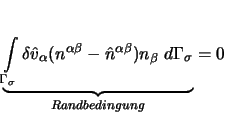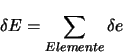Eine symbolische Lösung der Integration ist nur in einfachen Fällen möglich, in schwierigeren Fällen ist daher eine numerische Integration z.B. nach Gauß [Bathe 1990] notwendig.
zusammengebaut. ![]() ist hierbei der Unbekanntenvektor und
ist hierbei der Unbekanntenvektor und ![]() der Rechteseitevektor mit den Belastungen des Systems. Die aus den oben beschriebenen Anteilen der Integrale der Randbedingungen berechneten Vektoren werden in den Vektor
der Rechteseitevektor mit den Belastungen des Systems. Die aus den oben beschriebenen Anteilen der Integrale der Randbedingungen berechneten Vektoren werden in den Vektor ![]() eingebaut. Freiheitsgrade mit vorgegebenen Werten, wie z.B. vorgegebene Verschiebungen bei Aufgabenstellungen aus dem Bereich der Strukturmechanik oder vorgegebene Wasserhöhen bei Problemstellungen aus dem Bereich der Strömungsmechanik, und Belastungen des Systems sind analog zur Diskretisierung entsprechend den gewählten Ansatzfunktionen in den Vektor
eingebaut. Freiheitsgrade mit vorgegebenen Werten, wie z.B. vorgegebene Verschiebungen bei Aufgabenstellungen aus dem Bereich der Strukturmechanik oder vorgegebene Wasserhöhen bei Problemstellungen aus dem Bereich der Strömungsmechanik, und Belastungen des Systems sind analog zur Diskretisierung entsprechend den gewählten Ansatzfunktionen in den Vektor ![]() einzubauen. Zeilen und Spalten, bei denen der zugehörige Wert des Vektors
einzubauen. Zeilen und Spalten, bei denen der zugehörige Wert des Vektors ![]() Null ist, werden gestrichen. Das Gleichungssystem ist nun lösbar.
Null ist, werden gestrichen. Das Gleichungssystem ist nun lösbar.