


Nächste Seite: Partitionierungsalgorithmen
Aufwärts: Gebietszerlegungsverfahren
Vorherige Seite: Implizite Partitionierung:
Inhalt
Explizite Partitionierung:
Bei der expliziten Partitionierung wird das Netz, wie in Abbildung 2.14 demonstriert wird, zerteilt. Jeder Prozessor erhält ein Teilnetz, für das er das Gleichungssystem aufstellt.
Abbildung 2.14:
Substruktur-Technik
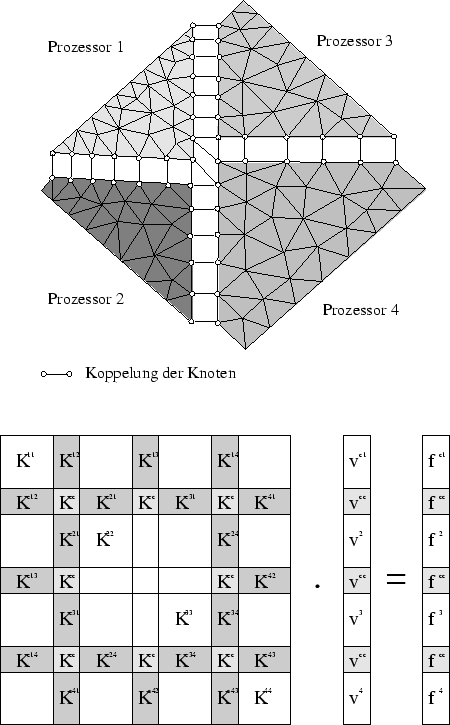 |
Ein Verfahren, welches hierfür gut geeignet ist, ist die Substruktur-Technik. Diese wurde entwickelt, um Problemstellungen, die zu groß für den Hauptspeicher waren, mit Hilfe der Finiten Elemente in mehreren Schritten zu lösen. Bei der Finite-Elemente-Berechnung auf einem Parallelrechner berechnet jeder Prozessor entsprechend der Substrukturtechnik das Gleichungssystem für die ihm zugewiesenen Elemente. Knoten entlang der Teilungsgrenzen bezeichnet man als Koppelknoten und sind auf jedem Prozessor vorhanden, der ein Element mit einem Koppelknoten besitzt.
Folgende Schritte sind bei der parallelen Berechnung erforderlich:
- Schritt 1:
- Aufstellen und Lösen des Gleichungssystems mit Dirichletscher Randbedingung an den Koppelknoten
- Schritt 2:
- Aufstellen des Koppelknotensystems
- Schritt 3:
- Berechnen des Koppelknotensystems
- Schritt 4:
- Berechnung im Inneren der Teilgebiete unter Berücksichtigung der Lösung für die Koppelknoten
