


Nächste Seite: Graphenbasierte Algorithmen
Aufwärts: Geometrische Algorithmen
Vorherige Seite: Koordinaten-Bisektion
Inhalt
Hauptachsenmethode
Die Hauptachsenmethode (siehe [Farhat und Lesoinne 1993], [Nour-Omid u. a. 1987], [Belkhale und Prithviraj 1990], [Simon 1991], [Chrisochoides u. a. 1994a]) teilt das Gebiet entlang der Hauptachse, die das größere Flächenträgheitsmoment aufweist. Die Achsen können aus den Eigenvektoren der Matrix
![\begin{displaymath}
I=\left[
\begin{array}{lll}
I_{xx}&I_{xy}\\
I_{yx}&I_{yy}
\end{array}\right]
\end{displaymath}](img40.gif) |
(6) |
bestimmt werden. Die Matrixelemente lassen sich mit Hilfe des Gaußschen Integralsatzes berechnen. Eine Koordinatentransformation in den Schwerpunkt ist notwendig.
Schwerpunktskoordinaten:
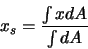 |
(7) |
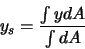 |
(8) |
Die Trägheitsmomente berechnen sich dann wie folgt:
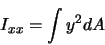 |
(9) |
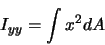 |
(10) |
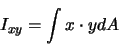 |
(11) |
Abbildung 2.16:
Hauptachsen Bisektion: a) zwei Teilgebiete, b) vier Teilgebiete, c) acht Teilgebiete
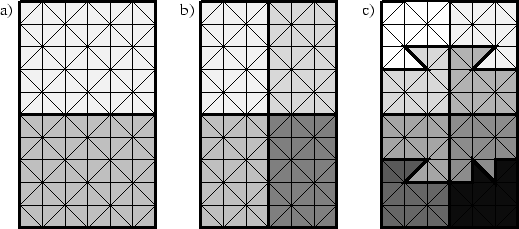 |
Der numerische Aufwand der Partitionierung ist wegen der Berechnung der Integrale wesentlich höher als bei der Koordinaten-Bisektion. Dieser höhere Aufwand rechtfertigt sich durch die wesentlich günstigeren Formen der Teilgebiete, die eine geringere Länge der Außenkante besitzen und daher weniger Kommunikationsaufwand während der nachfolgenden Berechnung bewirken [Lämmer 1997](siehe Abbildung 2.16). Eine Verbesserung der Partitionierung ist mit der Kernighan-Lin-Heuristik [Kernighan und Lin 1970] und dem Algorithmus der Hilfreichen Mengen [Diekmann u. a. 1994] möglich.



Nächste Seite: Graphenbasierte Algorithmen
Aufwärts: Geometrische Algorithmen
Vorherige Seite: Koordinaten-Bisektion
Inhalt
![\begin{displaymath}
I=\left[
\begin{array}{lll}
I_{xx}&I_{xy}\\
I_{yx}&I_{yy}
\end{array}\right]
\end{displaymath}](img40.gif)
![\begin{displaymath}
I=\left[
\begin{array}{lll}
I_{xx}&I_{xy}\\
I_{yx}&I_{yy}
\end{array}\right]
\end{displaymath}](img40.gif)
