 |
Der wichtigste Vertreter der graphenbasierten Algorithmen ist der Greedy-Algorithmus. Der Algorithmus wird in [Farhat 1988] und [Al-Nasra und Nguyen 1991] näher beschrieben.
Der Algorithmus teilt ein Gebiet im Gegensatz zu den rekursiven Algorithmen in beliebig viele Teilgebiete. Der Algorithmus lässt sich wegen der graphenbasierten Vorgehensweise für eindimensionale, zweidimensionale und dreidimensionale Gebiete anwenden. Durch seinen internen Aufbau und durch Abbruchkriterien bei der Generierung der Teilgebiete garantiert er Teilgebiete mit gleicher Anzahl von Elementen.
Der Algorithmus weist zu Beginn jedem Knoten des Netzes eine Wichtung zu, die der Anzahl der an ihn grenzenden Elemente entspricht. Danach werden nacheinander für jedes Teilgebiet folgende Schritte ausgeführt:
Für die Zuweisung der Elemente zu den Teilgebieten benötigt man eine Datenstruktur, die in den meisten Finiten-Elemente-Programmen nicht vorliegt. Jeder Knoten muss Zeiger auf die auf ihn referenzierenden Elemente haben und jedes Element sollte ohne Aufwand seine Nachbarelemente finden.
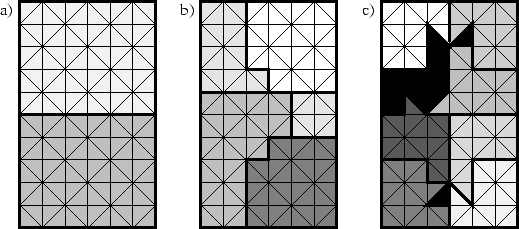
Für die ersten Teilgebiete wird eine Optimierung der Gebietsform und der Kantenlängen erreicht. Diese haben normalerweise eine etwa quadratische Form und somit eine minimale Anzahl von Koppelknoten. Hierdurch wird eine Minimierung der Kommunikation dieser Teilgebiete erreicht. Die zuletzt entstehenden Teilgebiete können aus mehreren Teilen bestehen, wie es in Abbildung 2.17 c) mit dem schwarzen Teilgebiet demonstriert wird. Dieses Teilgebiet besteht aus mehreren Teilen und hat daher eine unnötig hohe Anzahl von Koppelknoten. Das Verhältnis zwischen inneren Knoten und Koppelknoten ist ungünstig. Die Kommunikation mit relativ vielen anderen Prozessoren ist notwendig [Burghardt 1995], [Lämmer 1997].