Radial-Sweept-Algorithmus:

Der Radial-Sweept-Algorithmus ist der am einfachsten zu programmierende Algorithmus und wurde erstmals von [Mirante und Weingarten 1982] vorgestellt. Der Algorithmus besteht aus folgenden Schritten:

Abbildung 3.6: Radial-Sweept-Algorithmus

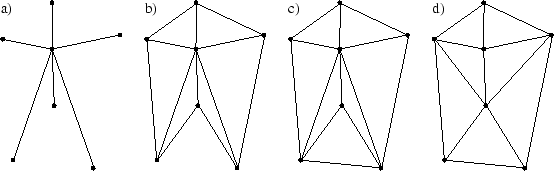Schritt 1:

Der dem Mittelpunkt der Geometrie am nächsten liegende Punkt wird ausgewählt und mit allen übrigen Punkten verbunden. Die Entfernung und Richtung zu den restlichen Punkten werden festgestellt und die Punkte nach der Richtung sortiert (Abbildung 3.6a)). Die äußeren Punkte werden entsprechend der Sortierung miteinander verbunden (Abbildung 3.6b)).

Schritt 2:

Die Außenkante des Gebiets wird traversiert. Bilden drei aufeinander folgende Punkte ein außenliegendes Dreieck, so sind diese in die Geometrie einzubinden (Abbildung 3.6c)).

Schritt 3:

Über alle Kanten wird traversiert. Die beiden durch diese Kante benachbarten Dreiecke werden zu einem gedachten Viereck zusammengefasst. Entlang der kürzeren Kante wird das Vierecke in zwei Dreiecke zerteilt. Dieser Schritt wird solange wiederholt bis keine Änderungen mehr auftreten (Abbildung 3.6d)).

Die beschriebene Vorgehensweise hat Nachteile im Laufzeitverhalten. Das Bestimmen der Richtungen der benachbarten Punkte ist sehr zeitaufwendig. In der Literatur gibt es hierfür Angaben über das Laufzeitverhalten von 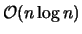${\cal O}(n \log n)$. Ebenfalls ungünstig wirkt sich das Traversieren aller Kanten auf die Laufzeit mit 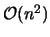${\cal O}(n^2)$ aus. Eine Parallelisierung der Richtungsbestimmung der Punkte sowie der Traversierung der Kanten ist denkbar, in beiden Fällen sind jedoch aufgrund der notwendigen Kommunikationen keine guten Effizienzen zu erwarten.