


Nächste Seite: Modified-hierarchical-Algorithmus:
Aufwärts: Statische Algorithmen
Vorherige Seite: Radial-Sweept-Algorithmus:
Inhalt
Step-by-Step-Algorithmus:
Der Step-by-Step-Algorithmus ist der wohl am häufigsten verwendete Algorithmus zur Erzeugung von Delaunay-Triangulierungen. Er wird unter anderem von [McCullagh und Ross 1980] beschrieben und verdeutlicht durch die Art der Generierung schon das Kreis-Kriterium.
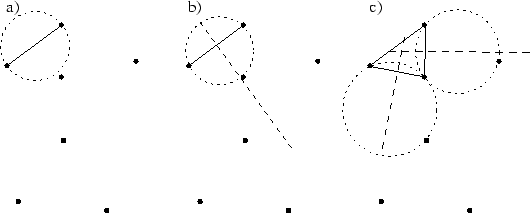
Abbildung 3.7:
Step-by-Step-Algorithmus
 |
- Schritt 1:
- Eine initiale Dreieckkante am Rand der Geometrie wird gesucht.
Im Kreis mit dem Mittelpunkt in der Mitte zwischen den beiden Punkten der Kante sollte kein weiterer Punkt liegen (Abbildung 3.7 a)).
- Schritt 2:
- Entlang der Mittelsenkrechten der Kante wird der Kreis verschoben und dabei der Radius angepasst. Der erste Punkt, der innerhalb bzw. auf dem Kreis liegt, erfüllt das Kreis-Kriterium (Abbildung 3.7 b)). Der gefundene Punkt und die beiden Punkte der initialen Kante werden die Eckpunkte des neuen Dreiecks.
- Schritt 3:
- Die neu eingefügten Kanten sind die initialen Kanten und der Schritt 2 wird rekursiv wiederholt.
Das Suchen der Punkte in der Nähe der initialen Kante erweist sich als ungünstig für das Laufzeitverhalten. Die Komplexität dieses Suchens ist mit
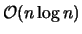 anzugeben, die Generierung der Dreiecke selbst nur mit
anzugeben, die Generierung der Dreiecke selbst nur mit 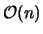 . Eine Parallelisierung dieses Algorithmus wird in [Saxena u. a. 1990] vorgestellt.
. Eine Parallelisierung dieses Algorithmus wird in [Saxena u. a. 1990] vorgestellt.



Nächste Seite: Modified-hierarchical-Algorithmus:
Aufwärts: Statische Algorithmen
Vorherige Seite: Radial-Sweept-Algorithmus:
Inhalt

![]() anzugeben, die Generierung der Dreiecke selbst nur mit
anzugeben, die Generierung der Dreiecke selbst nur mit ![]() . Eine Parallelisierung dieses Algorithmus wird in [Saxena u. a. 1990] vorgestellt.
. Eine Parallelisierung dieses Algorithmus wird in [Saxena u. a. 1990] vorgestellt.