


Nächste Seite: Dynamische Algorithmen
Aufwärts: Statische Algorithmen
Vorherige Seite: Step-by-Step-Algorithmus:
Inhalt
Modified-hierarchical-Algorithmus:
Dieser Algorithmus wird von [Floriani u. a. 1984] vorgestellt. Der Algorithmus ist eine Mischung aus dem Radial-Sweept-Algorithmus und dem Incremental-Algorithmus.
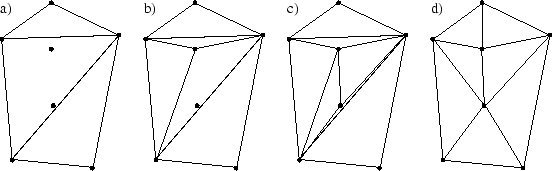
Abbildung 3.8:
Modified-hierarchical-Algorithmus
 |
- Schritt 1:
- Eine initiale grobe Vernetzung wird erzeugt z.B. durch Triangulierung des umschließenden Polygonzugs (Abbildung 3.8 a)).
- Schritt 2:
- Jeder in einem Dreieck liegende Punkt wird in das Netz eingebaut, indem das Dreieck durch drei neue Dreiecke, bestehend aus dem einzubindenden Punkt und den alten Punkten des Dreiecks, erzeugt wird (Abbildung 3.8 b), c)).
- Schritt 3:
- Über alle Kanten wird traversiert. Die beiden durch eine Kante benachbarten Dreiecke werden zu einem gedachten Viereck zusammengefasst. Entlang der kürzeren Kante wird das Viereck in zwei Dreiecke zerteilt. Dieser Schritt wird solange wiederholt, bis keine Änderungen mehr auftreten (Abbildung 3.8 d)).
Die Komplexität dieses Algorithmus hat die schlechteste Performance mit 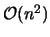 . Schritt 3 dieses Algorithmus ist parallelisierbar, indem die initialen Dreiecke den einzelnen Prozessoren zugeordnet werden. Durch die möglicherweise ungleiche Anzahl von in das Dreieck einzubindenden Punkten sind schlechte Effizienzen zu erwarten.
. Schritt 3 dieses Algorithmus ist parallelisierbar, indem die initialen Dreiecke den einzelnen Prozessoren zugeordnet werden. Durch die möglicherweise ungleiche Anzahl von in das Dreieck einzubindenden Punkten sind schlechte Effizienzen zu erwarten.



Nächste Seite: Dynamische Algorithmen
Aufwärts: Statische Algorithmen
Vorherige Seite: Step-by-Step-Algorithmus:
Inhalt

![]() . Schritt 3 dieses Algorithmus ist parallelisierbar, indem die initialen Dreiecke den einzelnen Prozessoren zugeordnet werden. Durch die möglicherweise ungleiche Anzahl von in das Dreieck einzubindenden Punkten sind schlechte Effizienzen zu erwarten.
. Schritt 3 dieses Algorithmus ist parallelisierbar, indem die initialen Dreiecke den einzelnen Prozessoren zugeordnet werden. Durch die möglicherweise ungleiche Anzahl von in das Dreieck einzubindenden Punkten sind schlechte Effizienzen zu erwarten.