Viereckelemente

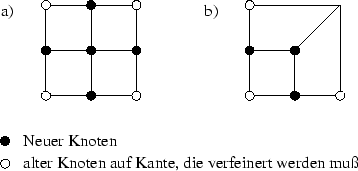
Die Verfeinerung von Viereckelementen ist wesentlich aufwendiger als die Verfeinerung von Dreieckelementen oder Tetraederelementen. Man muss zwei Arten von Verfeinerungen unterscheiden: die zweier-Verfeinerung und die dreier-Verfeinerung.

**Abbildung:** *Übergangsnetze der zweier-Verfeinerung von Vierecken*
$\begin{figure} \centerline {\psfig{figure=netz/bank3.eps}} \end{figure}$

Die zweier-Verfeinerung von Viereckelementen beschreibt [Kinney 1997]. Sie bedeutet, dass die betroffenen Kanten in der zu verfeinernden Region in jeweils zwei Teile geteilt werden. Bei dieser Art von Verfeinerung ist nur ein Übergangsnetz möglich. Dieses teilt zwei aneinander angrenzende Kanten (Abbildung 3.20 b)). Ein komplett verfeinertes Element ist in Abbildung 3.20 a) dargestellt.

Dieses nur eine mögliche Übergangsnetz bringt starke Einschränkungen für die Verfeinerung der Netze mit sich. Es ist nicht möglich beliebige Verfeinerungen in ein Netz einzubringen, da immer Paare von zu verfeinernden Kanten entlang der Außenkante der Verfeinerung gefunden werden müssen. In strukturierten Netzen ist dies oft möglich, in unstrukturierten Netzen sind mögliche Randpolygone mit gerader Anzahl von Polygonkanten nicht immer auffindbar.

Beliebige Verfeinerungen können in unstrukturierte Vierecknetze nur mit Hilfe der dreier-Verfeinerung eingebracht werden. Bei der dreier-Verfeinerung wird jede Elementkante in jeweils drei Teilkanten unterteilt [Schneiders 1996b].

**Abbildung:** *Übergangsnetze der dreier-Verfeinerung von Vierecken*
$\begin{figure} \centerline {\psfig{figure=netz/vier_rs.eps}} \end{figure}$

Zum Einbau beliebiger Verfeinerungen in unstrukturierte Vierecknetze sind die in Abbildung 3.21 b) - e) dargestellten Übergangsnetze notwendig. Zur Verfeinerung müssen zuerst alle Knoten der Elemente markiert werden, die komplett (Abbildung 3.21 f)) verfeinert werden sollen. In einem nächsten Schritt müssen die jeweiligen Verfeinerungsnetze (Abbildung 3.21 b) -e)) in Abhängigkeit der Kanten gesucht werden, die am Rand des Verfeinerungsgebietes notwendig sind.

Ein rekursives Vorgehen, das heißt ein mehrfaches Verfeinern an einer Stelle, ist problemlos möglich, indem der Verfeinerungsalgorithmus mehrmals hintereinander auf das Netz angewendet wird. Hierdurch erhält man je nach Rekursionsanzahl verschieden stark verfeinerte Elemente. Bei der verwendeten dreier-Verfeinerung wird ein Element durch maximal neun Elemente ersetzt, nach zwei Rekursionsschritten erhält man schon 81 und nach drei Schritten sind es schon 729 Elemente. Eine mehrfache Verfeinerung an einer Stelle ist immer mit Bedacht anzuwenden, da die Gesamtelementanzahl rapide steigen kann. In Abbildung 3.23 a) ist ein Netz dargestellt, das an einer Stelle einmal und an einer anderen Stelle zweimal verfeinert wurde. Die Gesamtanzahl der Elemente änderte sich durch diese Verfeinerungen von 48 auf 422.

**Abbildung 3.22:** *Ablauf der lokalen Verfeinerung von Netzen*
$\begin{figure} \centerline {\psfig{figure=2D/struk.eps}} \end{figure}$

Zur rekursiven Verfeinerung sind die in Abbildung 3.22 dargestellten Schritte notwendig. Zuerst werden alle Knoten an den zu verfeinernden Kanten mit der Anzahl der notwendigen Verfeinerungsschritte markiert (Abbildung 3.24 a). Danach sind folgende Schritte für jeden Rekursionsschritt der Verfeinerung notwendig:

Abbildung 3.23: Verfeinerung Viereckelemente, a) Netz, b) Form-Kriterium, c)Topologie-Kriterium

$\textstyle \parbox{45mm}{ a)}$ $\textstyle \parbox{45mm}{ b)}$ $\textstyle \parbox{45mm}{ c)}$ $\textstyle \parbox{45mm}{ \psfig{figure=2D/v5_netz.ps,width=40mm}}$ $\textstyle \parbox{45mm}{{ \psfig{figure=2D/v5_bw.ps,width=40mm}}}$ $\textstyle \parbox{45mm}{{ \psfig{figure=2D/v5_bw_form.ps,width=40mm}}}$

Im Bereich des Übergangs von groben zu feineren Elementen ist die Qualität der Elemente relativ ungünstig. Bei einem optimalen Ausgangsnetz, das nur Elemente mit Innenwinkeln von

$^{^{\tt\circ}}$ und jeweils gleicher Seitenlänge besitzt, erhält man Elemente mit Innenwinkeln von

$^{^{\tt\circ}}$ und Seitenlängen im Verhältnis

. Eine Darstellung der Qualität mit Hilfe des Form-Kriteriums (siehe Abschnitt 3.4) ist in Abbildung 3.23 b) zu sehen. Hierbei zeigen dunkel markierte Elemente eine schlechte Qualität an. Im dargestellten Beispiel sind diese Elemente nur im Bereich der Verfeinerung zu finden. Das Topologie-Kriterium (Abbildung 3.23 c), siehe Abschnitt 3.4), zeigt ebenfalls die Problematik auf. Im Bereich des Übergangs treten Knoten mit einer Anzahl von angrenzenden Elementen ungleich der optimalen Anzahl auf. So ist die Anzahl der an einen Knoten angrenzenden Elemente im Bereich der Verfeinerung von Viereckelementen teilweise sechs oder sieben, was einem Innenwinkel von

$^{^{\tt\circ}}$ bzw.

$^{^{\tt\circ}}$ entspricht.

**Abbildung 3.24:** *Rekursive Verfeinerung*
$\begin{figure} \centerline {\psfig{figure=2D/rek_verf.eps}} \end{figure}$