Vorgehensweise

Der im Rahmen dieser Arbeit verwendete Ansatz zur Parallelisierung eines Netzgenerators arbeitet wie folgt:

Teilen der Geometrie:

Die Geometrie wird, wie in Abbildung 4.1 dargestellt, rekursiv mit der Schwerachsenmethode [Farhat und Lesoinne 1993] in $n$ Schritten in $2^n$ Teilgebiete geteilt. Eine Teilung in zwei etwa gleich große Teilgebiete wird in jedem Rekursionsschritt erreicht. Die Qualität der Teilung ist problemabhängig und wird durch die Dichtefunktion, die die Elementgrößen beschreibt, gesteuert. Die Teilung läuft während des Programmablaufes parallel für alle Prozessoren ab, wobei jeder Prozessor sein eigenes Teilgebiet berechnet. Für die Gebietszerlegung ist daher keine Kommunikation zwischen den Prozessoren notwendig.

Abbildung 4.1: Rekursives Teilen mit der Schwerachsenmethode

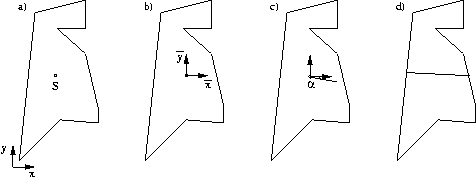
Die Diskretisierung des Randes, aller Polygone und aller Linien wird entsprechend der Verteilungsfunktion (Gleichungen 4.6 und 4.7) durchgeführt. Danach wird der Schwerpunkt der Geometrie mit den Koordinaten $x_s$ und $y_s$ bestimmt und eine Koordinatentransformation des Ursprungs in den Schwerpunkt vorgenommen. Die Eigenvektoren der Flächenträgheitsmomente $I_x$ und $I_y$ sowie der Deviationsmomente $I_{xy}$ und $I_{yx}$ ergeben die Schnittachsenrichtung. Die Geometrie wird nun entlang der Schnittachse geteilt, wobei der Rand nur an vorher vorhandenen Knoten geschnitten werden darf, wodurch die Kommunikation zwischen den Prozessoren vermieden wird. Hierdurch kann es zu Knicken in der Schnittlinien kommen.

Festlegung der Koppelknoten:

Nach jeder Teilung der Geometrie wird die Diskretisierung auf den Koppelrändern festgelegt, sodass während der Netzgenerierung keine Kommunikation notwendig ist. Das ist auch der Grund, warum eine Anwendung der Methode bei der Erzeugung von dreidimensionalen Hexaedernetzen nicht möglich ist. Hexaedernetze lassen sich nicht mit einer vorgegebenen Randdiskretisierung erstellen.

Generierung der Teilnetze:

In einem letzten Schritt wird nun parallel auf allen Prozessoren ein Netz für das Teilgebiet mit einem sequentiellen Netzgenerator erzeugt. Durch die vorgegebene Randdiskretisierung ist eine Kompatibilität der Elemente automatisch gegeben.