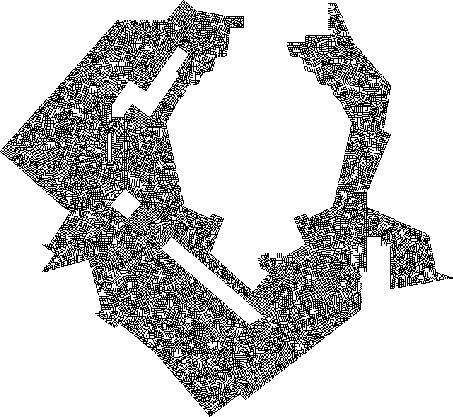 |
Mit der Diskretisierung 2 wird eine wesentlich feinere Auflösung des Netzes angestrebt. Die Kantenlängen betragen etwa 1 Meter, woraus sich eine Gesamtanzahl von etwa 16500 Elementen ergibt. Die Diskretisierung für einen Prozessor ist in Abbildung 7.5 dargestellt. Die Partitionierungen für mehrere Prozessoren entsprechen mit minimalen Abweichungen aufgrund einer anderen Randdiskretisierung den Partitionierungen der Diskretisierung 1.
Bei der rekursiven Teilung der Platte ergibt sich wieder das Problem der großen Öffnung. Die feinere Diskretisierung am Rand aufgrund der feineren Netzdichte bewirkt eine etwas günstigere Teilung der Geometrie bei der ersten Teilung als bei der Diskretisierung 1. Das Verhältnis der Elementanzahlen für zwei Prozessoren ist hier 54% zu 46 %. Die weiteren Teilungen sind wiederum günstiger als die erste. Nach vier Teilungen hat das kleinste Teilgebiet 67% der Elemente des größten Teilgebietes. Die feinere Diskretisierung und damit die höhere Auflösung des Geometrierandes bewirken ein exakteres Treffen der Schwerachsen. Die Teilung der Geometrie ist dadurch besser und die Elementanzahlen in den Teilgebieten ausgeglichener.