


Nächste Seite: Lastverteilungsfunktion
Aufwärts: Parallele Netzgenerierung
Vorherige Seite: Teilung der Geometrie
Inhalt
Geometrieverarbeitung
Beim Teilen der Geometrie ist es notwendig festzustellen, welche Teile der Originalgeometrie weiter verwendet werden. Hierfür muss überprüft werden, auf welcher Seite des Teilungspolygons ein Punkt, eine Kante oder ein Loch liegen.
Die hierfür notwendigen geometrischen Überprüfungen werden im Folgenden dargestellt:
- Punkt auf Punkt:
- Zur Überprüfung, ob zwei Punkte an der selben Stelle liegen, ist es notwendig dem zu überprüfenden Punkt P eine
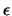 -Umgebung zuzuweisen, innerhalb derer alle weiteren Punkte als geometrisch gleich angesehen werden. In Abbildung 4.4 ist die
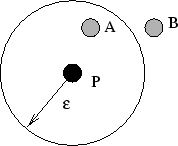
-Umgebung zuzuweisen, innerhalb derer alle weiteren Punkte als geometrisch gleich angesehen werden. In Abbildung 4.4 ist die 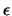 -Umgebung des Punktes P dargestellt. Punkt A wird als geometrisch gleich angesehen, da er in der
-Umgebung des Punktes P dargestellt. Punkt A wird als geometrisch gleich angesehen, da er in der 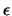 -Umgebung liegt, der Punkt B nicht. Bei der Überprüfung wird das Quadrat des Abstands der Punkte mit Hilfe des Satzes von Pythagoras bestimmt und mit dem Quadrat von
-Umgebung liegt, der Punkt B nicht. Bei der Überprüfung wird das Quadrat des Abstands der Punkte mit Hilfe des Satzes von Pythagoras bestimmt und mit dem Quadrat von 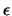 verglichen. Die Ermittlung eines Wertes für
verglichen. Die Ermittlung eines Wertes für 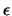 muss in Abhängigkeit der Abmessungen der Geometrie geschehen.
muss in Abhängigkeit der Abmessungen der Geometrie geschehen.
Abbildung 4.4:
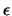 -Umgebung eines Punktes P
-Umgebung eines Punktes P
 |
- Punkt auf Linien:
- Die Überprüfung, ob ein Punkt auf einer Linie liegt, kann nur unter Zuhilfenahme einer
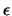 -Umgebung der Linie erfolgen. Diese Umgebung muss, wie in Abbildung 4.5 dargestellt, aus einer
-Umgebung der Linie erfolgen. Diese Umgebung muss, wie in Abbildung 4.5 dargestellt, aus einer 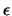 -Umgebung der Kante sowie den beiden
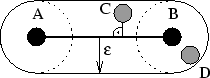
-Umgebung der Kante sowie den beiden 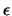 -Umgebungen der Punkte bestehen. Die Überprüfung ist daher zweigeteilt. Zum einen wird der Punkt-auf-Punkt Test für beide Endpunkte durchgeführt (Punkt D). Zum anderen wird der Lotfußpunkt des zu untersuchenden Punktes auf der Linie bestimmt (Punkt C). Falls dieser zwischen den Endpunkten liegt, wird das Quadrat des Abstands des Punktes und des Lotfußpunktes mit dem Quadrat von
-Umgebungen der Punkte bestehen. Die Überprüfung ist daher zweigeteilt. Zum einen wird der Punkt-auf-Punkt Test für beide Endpunkte durchgeführt (Punkt D). Zum anderen wird der Lotfußpunkt des zu untersuchenden Punktes auf der Linie bestimmt (Punkt C). Falls dieser zwischen den Endpunkten liegt, wird das Quadrat des Abstands des Punktes und des Lotfußpunktes mit dem Quadrat von 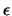 verglichen. Die Festlegung eines Wertes von
verglichen. Die Festlegung eines Wertes von 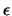 kann entweder in Abhängigkeit der Gesamtgeometrie oder in Abhängigkeit der Länge der Kante geschehen.
kann entweder in Abhängigkeit der Gesamtgeometrie oder in Abhängigkeit der Länge der Kante geschehen.
Abbildung 4.5:
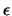 -Umgebung einer Linie
-Umgebung einer Linie
 |
- Punkt in Polygon:
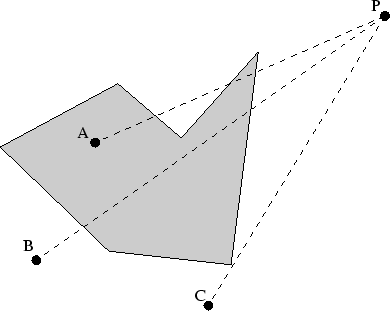
- Ob ein Punkt innerhalb eines Polygonzuges liegt, ist wesentlich aufwendiger festzustellen als die Durchführung der beiden oben dargestellten Tests. Zur Überprüfung wird ein Punkt P im Unendlichen erzeugt (siehe Abbildung 4.6). Von dem zu überprüfenden Punkt wird ein Strahl zum Punkt P gezogen und die Anzahl der geschnittenen Kanten ermittelt. Ist die Anzahl wie bei Punkt A ungerade, liegt der Punkt innerhalb des Polygons. Ist die Anzahl gerade wie bei Punkt B, liegt der Punkt außerhalb des Polygons. Der Strahl von Punkt C zum Punkt P geht durch einen Eckpunkt des Polygons. Hier ist eine Sonderbehandlung notwendig, da festgestellt werden muss, ob der Strahl den Polygonzug nur berührt oder ihn an dem Eckpunkt schneidet.
Abbildung:
Überprüfung Punkt in Polygon
 |



Nächste Seite: Lastverteilungsfunktion
Aufwärts: Parallele Netzgenerierung
Vorherige Seite: Teilung der Geometrie
Inhalt