 |
Die oben beschriebenen Verfahren zur Delaunay-Triangulierung können nur vorgegebene Punktmengen optimal zu Dreiecknetzen verbinden. Bei der Vorgabe der Außengrenze, von Fixpunkten und Löchern durch den Anwender ergeben sich nur sehr grobe, für die Finite-Elemente-Methode unbrauchbare Netze. Zum Generieren von Punkten innerhalb des Gebietes existieren eine Reihe von verschiedenen Generierungsalgorithmen. Mit Hilfe dieser ist es möglich Netze zu erzeugen, die der gewünschten Qualität und der angestrebten Elementgröße entsprechen.
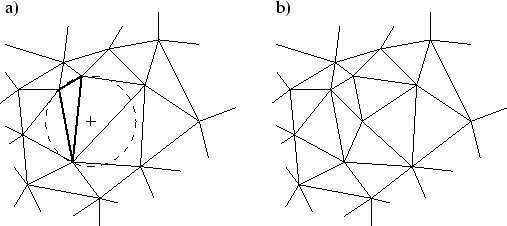
Ziel beim Einfügen von zusätzlichen Punkten in das Netzwerk ist das Eliminieren von Dreiecken mit schlechter Qualität. Bei Dreiecken mit schlechter Qualität liegt der Umkreis-Mittelpunkt weit außerhalb des Dreiecks (siehe auch Abschnitt 3.4). Die beschriebenen Dreiecke werden herausgesucht (Abbildung 3.11 a)). Alle Dreiecke, in deren Umkreis der Mittelpunkt des Umkreises des schlechten Dreiecks liegt, werden gelöscht. Der Umkreis-Mittelpunkt wird als neuer Punkt eingefügt. Aus jeweils zwei Eckpunkten der gelöschten Dreiecke und dem Mittelpunkt werden neue Elemente generiert (Abbildung 3.11 b)).