 |
Im Rahmen dieser Arbeit wird unter anderem die Delaunay-Triangulierung zur Netzgenerierung von Dreiecknetzen verwendet. Die Erläuterungen zu diesem Verfahren sind daher detaillierter als die Beschreibungen der anderen Verfahren.
Die Delaunay-Triangulierung ist in den letzten Jahren eine sehr populäre Methode zur Generierung von Netzen geworden. Sie existiert zum einen für zweidimensionale Dreiecknetze und zum anderen für dreidimensionale Tetraedernetze [Shewchuk 1997].
Die Delaunay Triangulierung optimiert den Innenwinkel der Dreieckelemente. Für zweidimensionale Netze findet der Algorithmus die optimale Vernetzung mit dem größtmöglichen minimalen Innenwinkel.
Delaunay-Netze werden über das Kreis-Kriterium definiert [Delaunay 1934]:
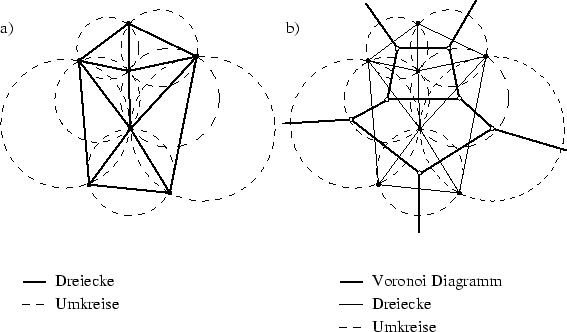
Bei der Existenz von nur drei Eckpunkten auf jedem Umkreis ist die Triangulierung eindeutig. Eine eindeutige Delaunay-Triangulierung ist beispielhaft in Abbildung 3.4 a) dargestellt. Der enge Zusammenhang mit den Voronoi-Diagrammen [Voronoi 1908] lässt sich aufzeigen und ist in Abbildung 3.4 b) dargestellt. Voronoi-Diagramme sind definiert durch die Senkrechte auf den Verbindungslinien zwischen zwei Punkten.
Eine Erweiterung der Theorie auf dreidimensionale Gebilde zur Generierung von Tetraedern ist möglich [Fuchs 1998]. Hierbei ist folgende Definition zu beachten:
Zur Generierung der Netze nach den oben beschriebenen Kriterien existieren eine Reihe von Methoden. Die Methoden zur Triangulierung lassen sich in zwei Gruppen teilen: die statische Triangulierung und die dynamische Triangulierung. Bei der statischen Triangulierung erreicht man im Gegensatz zur dynamischen das Kreis-Kriterium erst, wenn alle vorgegebenen Punkte im Netzwerk berücksichtigt sind.